General equation for non-equilibrium reversible-irreversible coupling (kinetic formulation)

Equations used by scientists and engineers can be classified into two larger groups: the first group includes deterministic and time-reversible equations, whereas the second includes irreversible and stochastic equations. Chemical kinetics equations belong to the second group, whereas the Hamilton equations of classical mechanics belong to the first group. Usually scientist work with equations of only one group, but sometimes it is needed to study situations that require elements of both classes at once; in such situations we need a new kind of equation that combines determinism, stochasticity, time-symmetry, and irreversibility all at once. Take the phenomenological equation for Brownian motion for the average momentum of a particle contained in a fluid, as illustration \[ \frac{\mathrm{d} p}{\mathrm{d}t} = F_\mathrm{ext} - \frac{\zeta}{m} p . \] The term \( F_\mathrm{ext} \) denotes the external deterministic and time-symmetric force, whereas the second term in the right-hand-side describes the irreversible force associated to friction with the fluid. This friction term has the characteristic form of kinetic equations. Since we are looking for a unified description of both terms, a first approach could be to write down the expression for \( F_\mathrm{ext} \) using the Hamiltonian formalism and then to obtain a similar expression for the irreversible term. Using the thermodynamics of moving bodies we find \[ \frac{\partial S}{\partial p} = - \frac{v}{T} , \] which helps us to rewrite the phenomenological equation of motion in a more unified fashion \[ \frac{\mathrm{d} p}{\mathrm{d}t} = - \frac{\partial E}{\partial x} + T\zeta \frac{\partial S}{\partial p} . \] This is the approach taken by the people behind the theory named GENERIC —acronym for General Equation for Non-Equilibrium Reversible-Irreversible Coupling—, which they write for generic state variables \( n \) as \[ \frac{\mathrm{d} n}{\mathrm{d}t} = L \frac{\partial E}{\partial n} + M \frac{\partial S}{\partial n} . \] Here \( L \) and \( M \) are two matrices associated to Hamiltonian flow and friction respectively, in fact \( M \) is named the friction matrix. The idea of extending the Hamiltonian formalism to irreversible phenomena is very interesting, but unfortunately most irreversible process are not so simple as the Brownian motion and the linear relationship between the generator of time-translations for dissipative processes and the gradient of entropy is lost. For instance for chemical reactions the generator is an exponential with the linear form only valid close to chemical equilibrium. For this reason expressions involving a dissipative potential \( \Xi \) have been proposed lately for GENERIC \[ \frac{\mathrm{d} n}{\mathrm{d}t} = L \frac{\partial E}{\partial n} + \frac{\partial \Xi}{\partial (\partial S/\partial n)} . \] Since chemical kinetic equations are known to describe well complex nonlinear phenomena, we will consider an alternative approach. Instead taking the Hamiltonian formalism as base to rewrite the friction term \( (\zeta/m) p \), we will take the kinetic formalism as base to rewrite the deterministic term \(F_\mathrm{ext}\), obtaining the next reformulation of the Brownian motion equation \[ \frac{\mathrm{d} p}{\mathrm{d}t} = \left( K - \frac{\zeta}{m} \right) p . \] Instead writing the concrete expression for \( K \), we will write directly the general equation for abstract state variables \( n \) \[ \frac{\mathrm{d} n}{\mathrm{d}t} = \Omega n \] and the relationship of the generator of time translations \( \Omega\) with the traditional formulation of GENERIC \[ \Omega_{\alpha\beta} = L_{\alpha\beta} \frac{\partial E}{\partial n_\beta} \frac{\partial}{\partial n_\beta} + M_{\alpha\beta} \frac{\partial S}{\partial n_{\beta}} \frac{\partial}{\partial n_\beta} . \] This is not the only possible way to write it. Another possibility that resembles a dissipative generalization of the Poisson brackets of classical mechanics is \[ \Omega_{\alpha\beta} = \frac{\partial E}{\partial n_\alpha} L_{\alpha\beta} \frac{\partial}{\partial n_\beta} + \frac{\partial S}{\partial n_\alpha} M_{\alpha\beta} \frac{\partial}{\partial n_\beta} . 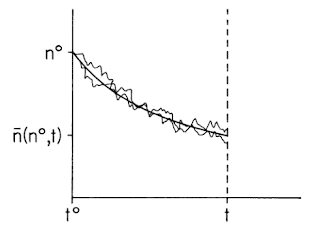\] But all the equations written up to now are deterministic. There are different ways to introduce fluctuations. A heuristic approach using a Fokker & Planck equation was used in the original paper of GENERIC, whereas a systematic approach based in projection operator techniques was used latter. I am exploring a novel approach to fluctuations. The starting point is the assumption that at some initial time \( t^0 \) the state is fully known \( n = n^0 = \overline{n} \), but fluctuations transform the state into a stochastic variable \( n = \overline{n} + \delta n \) at posterior times

We have to combine the pair of equations for the stochastic trajectories and the conditional average \[ \frac{\mathrm{d} \overline{n}}{\mathrm{d}t} = \overline{\Omega} \overline{n} \] \[ \frac{\mathrm{d} n}{\mathrm{d}t} = \Omega n . \] The result I got after some algebra is \[ \frac{\mathrm{d} n}{\mathrm{d}t} = \Omega n - \epsilon (n - \overline{n}), \] where \( \epsilon \) is a positive infinitesimal. Formally, this expression resembles the Zubarev equation used as foundation for an extension of statistical mechanics to irreversible processes, the physical interpretation is however different.