The Heisenberg uncertainty principle
The Heisenberg uncertainty principle is one of the most famous elements of quantum theory, not only mentioned in academic papers and described in quantum mechanics textbooks, but also present in popular treatises. Well, the fact is that "Heisenberg uncertainty principle" is a misnomer because it is neither a principle nor about uncertainties.
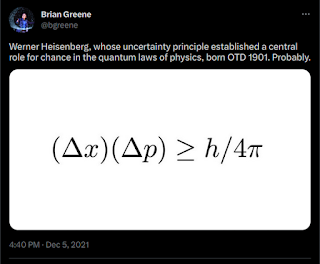
Brian Randolph Greene, a leading theoretical physicist, mathematician, and string theorist, often mentions the Heisenberg uncertainty principle. He does so in his popular books and he did again in a recent tweet.
The "Heisenberg uncertainty principle" is usually abbreviated as HUP and the first thing to clarify about it is that it is not a principle, but a theorem derived from the postulates of quantum mechanics. A derivation of this theorem can be found in book [1]. The result for two arbitrary quantum operators \( \hat{A} \) and \( \hat{B} \) associated to the observables \( A \) and \( B \) is
\[ \sigma(A) \cdot \sigma(B) \geq \frac{\vert\langle \hat{C} \rangle\vert}{2} \]Here \( \langle \hat{C} \rangle \) is the quantum average of the commutator \( \hat{C} = -i [ \hat{A} , \hat{B} ] \) and \( \sigma \) the standard deviation of the quantity. When two operators commute, \( \hat{C}=0 \), and the product of the standard deviations can be zero. When the operators do not commute the product must be greater than zero. A typical example of operators that do not commute are the position \( \hat{r} \) and momentum \( \hat{p} \) operators. Their commutator is \( [ \hat{r} , \hat{p} ] = ih/2\pi \), where \( h \) is Planck's constant, and the product of the standard deviations is \( \sigma(r) \cdot \sigma(p) \geq h/4\pi \). This is the result reproduced by Greene, but with a slightly different notation [2]. Another typical example are the angular momentum operators \( J_x \), \( J_y \), and \( J_z \), whose commutator is \( [ J_x,J_y ] = ih J_z/2\pi \).
What is the physical interpretation of this theorem? Uncertainty or indeterminacy? Uncertainty is a concept in measurement theory, while indeterminacy is an ontological concept in philosophy. Uncertainty implies that the exact values are not known or measured by us, although their existence is not in doubt; indeterminacy implies that the values do not exist. The uncertainty introduced by a wooden ruler does not prevent the objects on the table from having a well-defined location; however, a photon cannot be located because the position operator only exists for massive particles. The physical interpretation of this theorem is in terms of indeterminacy.
The result reproduced by Greene is traditionally associated with uncertainty, because Heisenberg himself introduced the concept in relation to perturbations in observed systems caused by measurements: "observation of the position will alter the momentum by an unknown and undeterminable amount" [3]. Even today, we can read statements like "when one performs a measurement on a microscopic system, one disturbs it in a fundamental fashion" in quantum mechanics textbooks. However, the inequalities proposed by Heisenberg have nothing to do with measurements. Those inequalities can be derived using only the algebra of operators and the properties of the quantum states of the system; the inequalities hold even without any measuring apparatus.
Since the 'HUP' is not a principle or related to uncertainty, the correct technical term would be indeterminacy relations. Those relations are a set of inequalities that impose a fundamental limit on the statistical dispersion of the values of certain pairs of physical quantities simultaneously assigned to a quantum state. The expression \( \sigma(r) \cdot \sigma(p) \geq h/4\pi \) does not mean that position or momentum will be disturbed by a measurement, but rather that a quantum ensemble cannot have both position and momentum simultaneously.
Of course, if the ensemble cannot have simultaneous values then we cannot measure them; but this has nothing to do with measurement disturbances since the system does not have simultaneous values before the measurement.
A "Heisenberg uncertainty principle for energy and time interval" [4] is often presented as having the same physical nature as the position-momentum indeterminacy relations, so the hypothetical inequality \( \sigma(t) \cdot \sigma(E) \geq h/4\pi \) is interpreted as the association of an uncertainty in energy to an uncertainty in time. Earlier we explained why such inequalities do not represent any uncertainty. Furthermore, there is no time operator in quantum mechanics and there can be no statistical dispersion for time \( \sigma(t) \) in analogy with the dispersions for position, momentum, or energy. It is possible to derive a time-energy relation from the first principles of quantum mechanics. The correct result is
\[ \tau \cdot \sigma(E) \geq \frac{h}{4\pi} \]For the derivation of this result and the physical interpretation of \( \tau \), see my forthcoming series of books on Common Misconceptions in Physics (in preparation).
REFERENCES AND NOTES
- Quantum Mechanics: A Modern Development 2000: World Scientific Publishing Co. Pte. Ltd., Singapore. Ballentine, Leslie E.
- I am using \( r \) to denote position in order to avoid confusion with the \( x \) coordinate. I am also using \( \sigma() \) for the standard deviation to avoid confusion with the operator \( \Delta \) that denotes the increase in a quantity.
- Nine formulations of quantum mechanics 2002: Am. J. Phys. 70(3), 288–297. Styer, Daniel F.; Balkin, Miranda S.; Becker, Kathryn M.; Burns, Matthew R.; Dudley, Christopher E.; Forth, Scott T.; Gaumer, Jeremy S.; Kramer, Mark A.; Oertel, David C.; Park, Leonard H.; Rinkoski, Marie T.; Smith, Clait T.; Wotherspoon, Timothy D.
- Sears and Zemansky’s university physics: with modern physics; Thirteen Edition 2012: Addison-Wesley; San Francisco. Young, Hugh D.; Freedman, Roger A.; Ford, A. Lewis (contributing author).