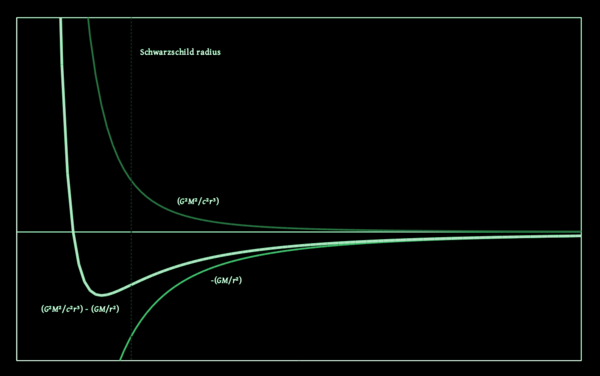
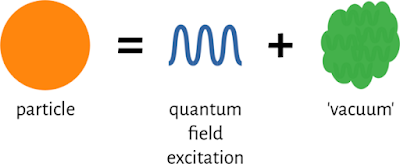
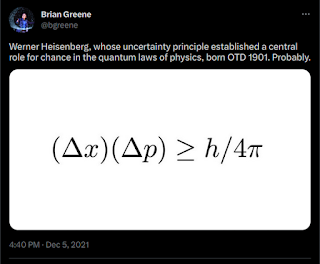
The demons haunting thermodynamics

In a recent Physics Today article [1], Katie Robertson wonders if the philosophical demons that haunt thermodynamics have been exorcised. She begins by stating that thermodynamics is a strange theory because although it is fundamental to our understanding of the world, it differs dramatically from other physical theories. I do not agree. First, thermodynamics is not a theory. Thermodynamics is a scientific discipline and, as in other sciences, we have theoretical, computational, and experimental flavors. Second, I do not know what she mean when she claims that thermodynamic theory differs dramatically from other physical theories. I do not find any fundamental difference with electrodynamics, with mechanics or with general relativity. In this newsletter, I will avoid "the bizarre philosophical implications" and focus on the scientific aspects. The "many oddities" that Robertson assigns to thermodynamics are actually oddities of statistical mechanics and, more speci...